Windows <Prev Next>

Log Window

This window is used to display the results of line position, line intensity, energy level or contour fits and will also display details of calculations if the PrintLevel is positive. It will typically appear automatically, or bring it up with View, Log. For line position and intensity fits, a line list giving details of each fitted rotational line, with an observed and calculated frequency or intensity and obs-calc for each line, is also given. For a graph of the residuals, see the Residuals Window. Note that the information displayed applies to one fit cycle; as a non-linear fitting process is used expect to fit several times until convergence is obtained. Click on an item in the picture below for more information:


Fit Details
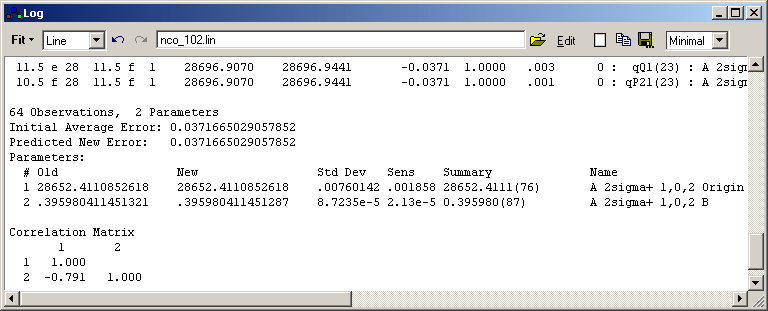
Observations
 		nobs  = The number of lines fitted or the number of experimental points for a contour fit
Parameters
 		npar = The number of parameters floated
Initial Average Error
 		This is [Σ[(obsi-calci)/wi]2/(nobs-npar)]½ with the calculated values, calci, obtained using the parameters at their initial values. wi are the estimated (relative) standard deviations of the observations.
Predicted New Error This is [Σ[(obsi-calci)/wi]2/(nobs-npar)]½ with the calculated values, calci, obtained from the non-linear least squares fit. They are typically close to the values that would be obtained from the new parameters, but are only exact if the calculated values are linear (or nearly linear) in the parameters. This is should be the case near to convergence, but often not when starting the fitting process. Fit again to find the true new error.
Old
 		The parameter value at the start of the fit.
New
 		The parameter value after the fit cycle.
Std Dev
 		The estimated standard deviation of the parameter, based on the quality of the fit.
Change/Std
 		(New-Old)/Std Dev - the relative change in the parameter.
Sens
 		Watson's sensitivity parameter (J. K. G. Watson, J. Mol. Spectrosc. 66, 500 (1977)) for the parameter. This is the change in the parameter that would make the average error of the fit increase by a factor of 0.1/npar, and provides a useful guide as to how many figures should be quoted for the parameter to ensure that the calculation can be reproduced. Where parameter correlation is high, this can be many more figures than suggested by the standard deviation of the parameter. See also R. J. Le Roy, J. Mol. Spectrosc. 191, 223 (1998) for discussion of this issue, and alternative approaches.
Deriv Diff
 		This column and the next are only shown if "Check Derivatives" is selected. This prompts for a multiple, c, and then for each parameter calculates a maximum difference in derivatives using the default increment, and the increment multiplied by c. Formally the derivative of a calculated value, y, with respect to a parameter, p, is worked out using:
dy/dp = (y(p+i)-y(p))/i
where i is the increment for the parameter. The value displayed here is the largest difference between derivatives calculated with increments i and i×c, looking over all observations. It is divided by the largest derivative for that parameter, again looking at all observations.
Obs#
 		The observation number of the largest derivative difference shown in the previous column.
Summary
 		The new parameter, with the one standard deviation in units of the last figure in brackets. The sensitivity is used to determine how many figures are displayed for the standard deviation.
Correlation Matrix The correlation between the parameters.

Buttons

Do fit of indicated type. For fits other than a Contour fit, the experimental information is taken from the file set at the top of the window. Alternatively, you can take the information from the clipboard by right clicking on the fit button. (This works well if you prefer to use Excel or another spreadsheet program to manage the experimental line list; before each fit select the required area of the spreadsheet and copy it to the clipboard.)
Line
 line position fit
Contour contour fit to current overlays
Intensity line intensity fit to line list in file shown
Fractional Intensity
 line intensity fit to line list in file shown, with weights taken as equal to the intensity.
ELower
 Fit to the lower state energy
EUpper
 Fit to the lower state energy
Calibration
 Calibration Fit
CDLower
 Lower state combination difference fit
CDUpper
 Upper state combination difference fit
This pops up a menu providing the following modified fits:
  • Fit Once - Do one fit cycle (The fit button above does FitCyles fits, though the default is one)
  • Fit Five Times - Do five fit cycles.
  • Check Derivatives - Do one fit cycle, showing extra information - see "Deriv Diff" above.
  • ShowResiduals - Do a complete fit cycle, including print-out, but do not float any parameters.
Step constants back one fit cycle for each press
Step constants forward one fit cycle
Click to browse for experimental file name
Edit given file; this button will normally start the Slave Editor
Clear log window
Copy log to clipboard.
Save log to file.

Select amount of log output on simulation or fitting. See PrintLevel for the possible values.